本文同步刊載於 [ECC 橢圓曲線密碼學：30 天從入門到入土] 前言

嗨大家，我是 Panda，平常偶爾會出現在各種 Conference 看看世界長點見識，這次鐵人賽是跟成大資安社牛肉湯的朋朋一起組隊，希望可以跟大家一起完賽。

以我的觀察，在臺灣打 CTF 的玩家，最少研究的應該是密碼學吧，也許是覺得學密碼學對實務上沒啥幫助，而事實上 Crypto 比起 Web Reverse Pwn Forensics 在 Real World 的漏洞確實少得多，我會想做這個主題就還是為了好玩啦，演算法在腦中流動的感覺還是挺不錯的，另外目前 AI 還沒辦法很穩定解出 CTF 的 Crypto 題，也能在之後打 CTF 時創造點優勢。

之所以會選擇 ECC 一方面是在 CTF 常見的幾種 Crypto 題目中（AES / RSA / ECC），就只有 ECC 我是沒什麼學過的，另一方面就是他的應用蠻廣的，比較常有機會跟別人 炫耀 分享說自己知道他們背後原理是什麼，像 TLS/SSL、加密貨幣的區塊鏈交易簽章、OpenSSH、WireGuard VPN 等等的，然後因為 ECC 金鑰比較小，運算比較快，所以也常用在 IoT 上，就想說趁這個機會好好學一下，免得每次都只是會跟別人打打嘴炮但其實背後原理一知半解XD

這個系列中，會以一個已經對 現代密碼學 有過基礎認識的初學者的角度，記錄學習橢圓曲線密碼學過程，要是文章的安排有點亂還請見諒，如果有寫錯的地方也歡迎大家指正，希望可以幫助到同樣對密碼學演算法有興趣的人們 owo/

最後關於題目，我在今天才發現好像應該叫橢圓曲線密碼學比較好，畢竟後面除了講加密外大部分應該都是說數位簽章，但因為組隊挑戰昨天就截止了，除非我重新報名否則鐵人賽的題目沒辦法改，就算了吧，不過每天的標題就還是會寫改成寫橢圓曲線密碼學比較符合內容。

我的環境

在這個系列中，我應該會主要用 Python 和 C++ 來實作，作業系統可能會是 MacOS 15.6 和 Fedora 42 交叉使用，但應該是不會有什麼影響。

初探 ECC 橢圓曲線密碼學

因為我英文不太好，又懶得看文字，就直接上 YouTube 上看看有沒有些資源可以參考

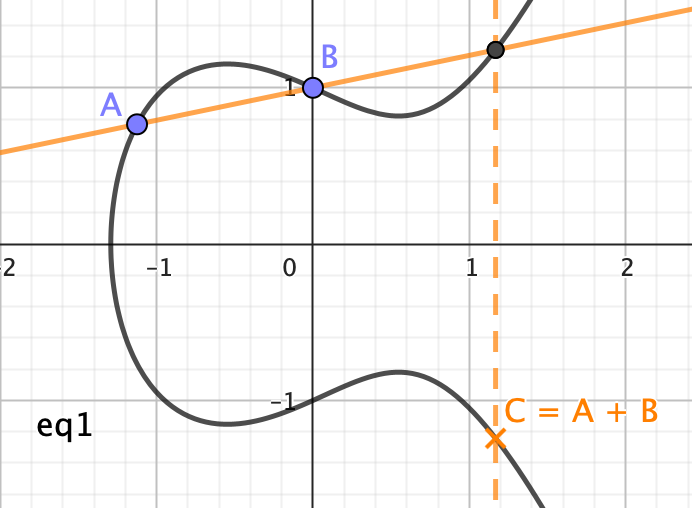
所以我就把兩部影片看完了，挺酷的，給定一條曲線： $y^2 = x^3 + ax + b$

為曲線上的點，定義一種特別的加法和乘法， $A+B=C$ 如下圖所示，$C$ 為過 $A$ 與 $B$ 直線，和曲線的交點對稱 X 軸後的點

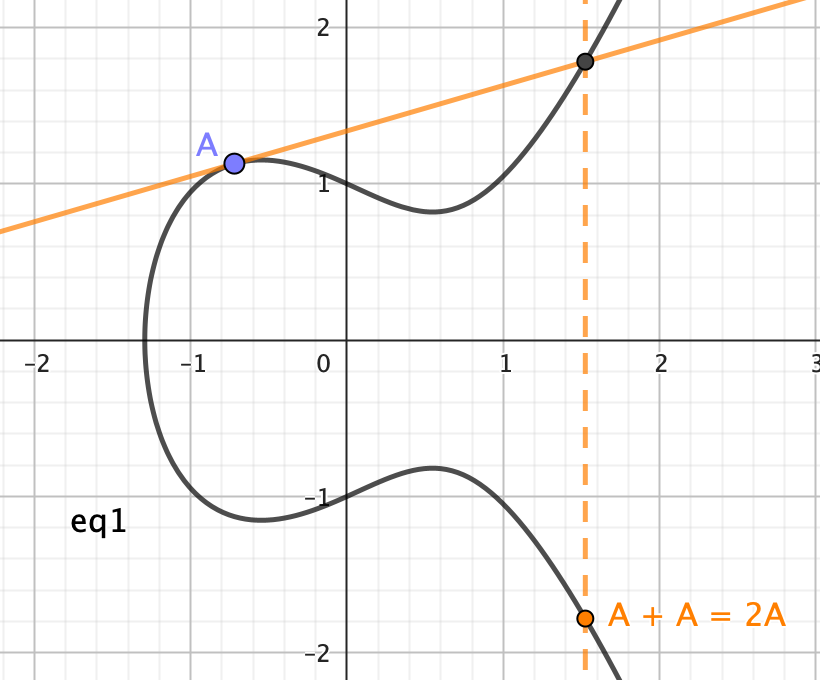
而 $A + A$ 就是 A 點切線與曲線的交點對稱 X 軸後的點，並定義這個點為 $2A$ 如下

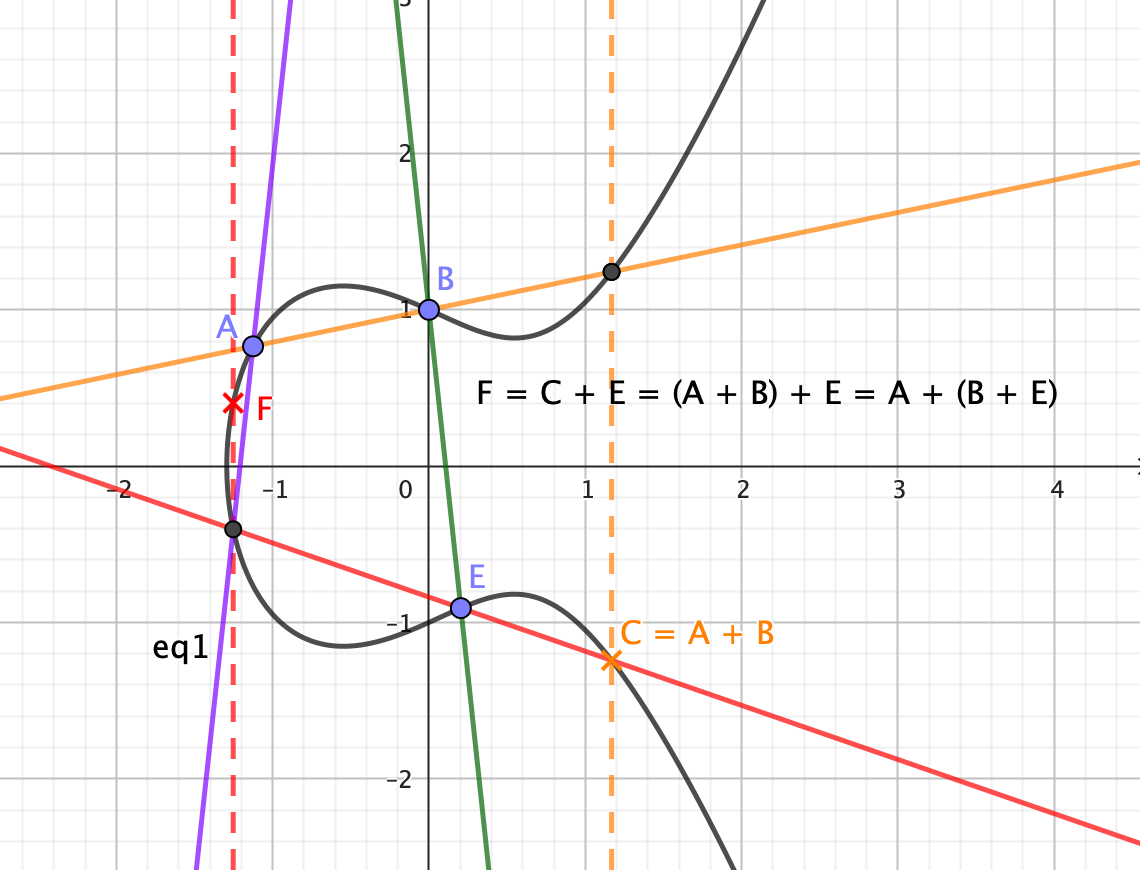
因為加法有結合律，所以明顯的 $3A = A + 2A$，$2A + 2A = 4A$，對 $kA$ 的那個點只需要做 $\log_{2} k$ 次的運算就能找到，這個小細節對後面講到時間效率時會有幫助。

而在加密時，他們可以用以下的方式創造出共同密鑰並通訊：

1. 對一個給定的曲線（即 $y^2 = x^3 + ax + b$ 的 $a, b$ 固定），和給定的點 $G$
2. Alice 和 Bob 各自生成私鑰 $a, b$ ($a, b$ 會是很大的數字)
3. Alice 和 Bob 互相傳遞 $aG$ 和 $bG$ 算出的點是什麼
4. 這時 Alice 可以算出 $a(bG)$ 而 Bob 可以算出 $b(aG)$ 而這個結果會是一樣的點，且除他們兩個外沒有其他人能運用 $G, aG, bG$ 算出
5. 運用這組密鑰做加密通訊

結語

今天就差不多到這裡，在初探了是怎麼使用橢圓曲線做加密後，下一步應該會想詳細看看他背後的數學原理，了解他的安全性，希望不要被數學打敗了，感謝大家 owo/

參考資料

• 公钥加密技术ECC椭圆曲线加密算法原理
• 椭圆曲线加密与哈希函数是什么？非对称加密是什么？比特币中的数学原理

本文同步刊載於 [ECC 橢圓曲線密碼學：30 天從入門到入土] 前言